Software Analysis System (SAS)
The launching by Intel in 1971 of the first microprocessor, the 4004, heralded the start of what was termed “The Microprocessor Revolution” – a rapid proliferation of computer applications due to the development of a low cost CPU fabricated on a single semi-conductor chip.
Since that moment there is no doubt that microprocessors have transformed the world by reaching into almost every facet of life, being key components embedded into almost all electronic appliances. For example, even though they don’t resemble computers, smart homes, smart phones, modern cars and aircraft etc, are all packed with microprocessors. However, in order to do useful things, microprocessors need software. Depending on the application, failure of this software could be anything from annoying to death threatening, so it’s important to have ways to measure the quality of software (its likelihood to remain working effectively). With some physical commodities it’s possible to assess the quality of the product by looking at it, but software is an abstract entity that is not possible to “look at” and assess in a conventional way. To assist in this process various tools such as logic analysers, signature analysis, debuggers and a myriad of other engineering tools have been constructed which, in expert hands, can give some insight to the quality of the software. On the other hand, mathematically minded researchers have come up with some formal mathematical tools to reason about the correctness of the software. Generally, these two approaches (electronic tools and formal methods) are uncomfortable bedfellows, rarely working together effectively. However, this research sought to unite these two separate streams of work to produce an engineering tool that exploited mathematical methods. The next section outlines the mathematical method used.
Complexity
This project was undertaken in the seventies, when there was a widespread belief that complexity was the enemy of reliability (or quality). A popular mantra of that time was “simplicity breeds reliability”. The view was the more simple the design, the less likely a designer was to make a mistake, or the more likely a designer was to predict all the possibilities. In the software field a popular way to limit program complexity was what was termed structured programming. In its most fundamental sense this meant writing program from only a specified set of program logical constructs. The decision structure of a program is very important as it governs the possible execution paths that a program may follow for any given conditions. One of the main difficulties in understanding or testing programs is determining and following the program path through complex decision logic. Professor E W Dykstra, in 1965, was the first person to formally suggest the value of structured programming. This idea was extended in 1966 by research which demonstrated that three basic control constructs, linear sequence, selection and iteration were sufficient to express any chartable flow logic (with structured programming being interpreted by some people in a somewhat simplistic notion of “No Goto statements“). Later a method of measuring the relative complexity of a program, based on calculating what was termed the cyclomatic number from the decision logic structure, was proposed by Thomas McCabe (McCabe 1976).
Cyclomatic Complexity
The cyclomatic measure defines the number of basic paths that, when taken in combination, will generate every possible path. McCabe chose this approach rather than attempting to calculate the total number of actual paths because any program which is either non-structured, or contains a backward branch, potentially can have an infinite number of paths! The cyclomatic number C(G) of a directed graph G, with n vertices, e edges and p connected components is (from graph theory) defined as:
C(G) = e – n + p
This is interpreted as follows; in a strongly connected graph (G), the cyclomatic number is equal to the maximum number of linearly independent circuits which, if taken in combination, will generate every possible path. Strongly connected means that there is a directed path between any two nodes on the graph. Often this implies the addition of a reverse branch (which, from above, can give rise to an infinite number of distinct paths!). To be able to use this complexity calculation with decision structures that are not strongly connected, an additional edge needs to be associated with the graphs entry and exit nodes. Thus, for such graphs the cyclomatic complexity formula becomes:
C(G) = e – n + 2p
Since an extra edge is added for each component/ McCabe emphasised that the process of adding an extra edge was only to make the cyclomatic theorem apply and that this extra edge is not an issue but rather that it is reflected in the expression used for complexity.
SAS
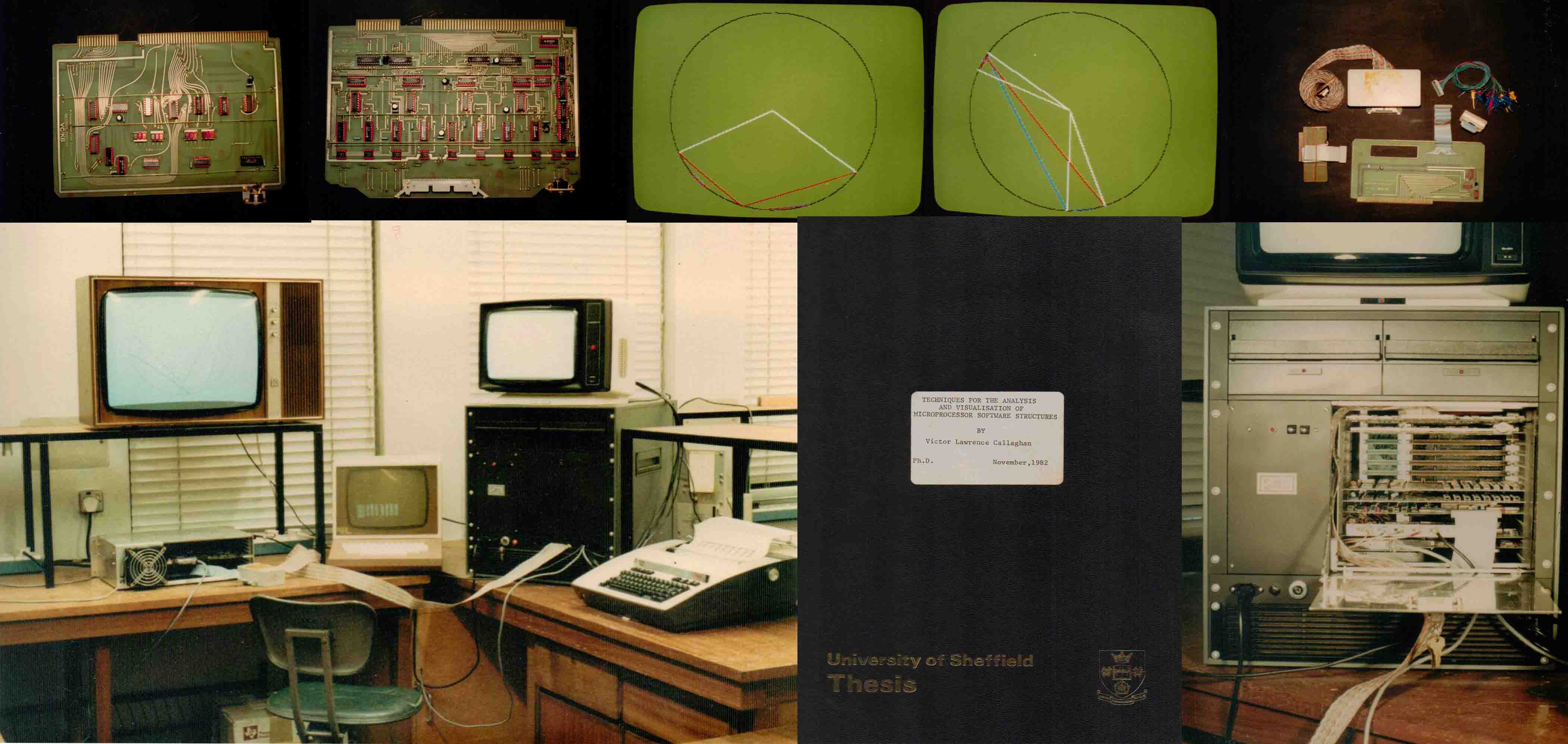
The breakthrough with SAS was the recognition that in McCabe’s cyclomatic complexity measure, the directed graph edges and nodes were equivalent to branch vectors and sources-destination addresses respectively. While this may seem a somewhat obvious association between theory and physical architecture, at the time this represented a major unification of engineering tools (that operate directly on hardware) and formal methods (that reason about complexity and computation with mathematics). Extracting branch vectors was a relatively simple hardware process as, in its most fundamental form, it amounted to detecting discontinuities in the program counter sequence (termed branch vectors). Once such branch vectors were accumulated, they contained a richness of information that went well beyond McCabe’s cyclomatic complexity number and revealed the hidden structure of all code, including the host operating system and any applications. By extending the technique to correlate external I/O events, or internal signalling, it was possible, to reverse engineer systems, or provide an alternative debugging strategies. As such SAS incorporated well over 50 operators, in addition to McCabe’s cyclomatic complexity measure. As SAS needed only to gather only unique branch vectors and their frequency of occurrence, the storage requirements were orders of magnitude less than trace based approaches, such as logic analysers. Also prior to this work, complexity measures were made on static code, whereas SAS moved this forward to provide an insight into dynamic structure, complexity and code usage (ie it highlighted the differences between what a programmer expected, and what the system did). Of course, this work was conducted at a point of computing history where mainframes and mini-computers were widespread and the microprocessor revolution was in its infancy. In fact the project had commenced by using a Varian minicomputer running an operating system called MP/3 (and an interpreter called VAMP/3) supported by Alcock Shearing & Partners (of 16/18 Station Road, Redhill, Surrey UK RH1 1NZ and better known as Euro-Computer Systems Ltd, Reg No. 01433940, which was incorporated on the 29/06/1979 and traded for 40 years and 7 months before being dissolved) who were the operating system authors (Brian Shearing and Donald Alcock). By way of illustrating the pace of the microprocessor revolution on the late seventies, the three year SAS project started on a mini-computer and ended using microprocessors (with the original Varian multi-user minicomputer being replaced by a lab of Texas Instruments TI9900 and Motorola 6800 microprocessors!). The photographs below show the original SAS system. The picture on the bottom left shows the SAS system in a lab monitoring software on a small TMS99000 Texas Instruments microprocessor (in the silver rack). The picture on the bottom right is of the main SAS chassis housing the branch vector acquisition boards (shown on the top left and right) and the analysis processors. Much of the analysis was output in the form of processed data but there were some real-time visual displays of structure maps, as shown in the circular diagrams on the top row. The red and blue colours indicate the directions of branch vectors and the intensity mirrors frequency (the white vectors are calibration vectors). Given the advances since the seventies, this equipment all looks somewhat dated but, if nothing else, it serves to illustrate the technology of those days (look at the two large 8” fluffy disc drives at the top – at the time this was an advanced microprocessor system, most of the microprocessor lab systems were using magnetic cassette tape for non-volatile storage!).
References:
- Callaghan V, Barker K “SAS – an experimental tool for dynamic program structure acquisition and analysis (HTML version) (PDF version)” (Historical Context Of SAS Paper), Elsevier, Journal of Microcomputer Applications, Volume 5, Issue 3, July 1982, Pages 209-223, ISSN 0745-7138, DOI: https://doi.org/10.1016/0745-7138(82)90003-3. (http://www.sciencedirect.com/science/article/pii/0745713882900033).
- Callaghan V “Techniques for the Analysis and Visualisation of Microprocessor Software Structures“, PhD Thesis, Sheffield University, November 1982 (supervised by Dr Keith Barker & Dr Doug Thomsit, Internal examiner Prof Frank Benson, external examiner Prof Mike Sterling).
- McCabe TJ “A Complexity Measure“, IEEE Transactions on Software Engineering, SE-2, No 4, December 1976, pp308-320